量化
模型量化是指将神经网络模型中的连续取值的权重或激活值近似为有限多个离散值的过程。
量化原理与优劣
将Float32的参数转换为INT8,在节省内存的同时能够节省计算
- 压缩参数:使用低精度整型数据表示原来的高精度浮点数据,可以减少存储参数所需的空间。
- 提升速度:当权重与激活全部量化为整型值后,就可以将原来的浮点运算转换为高效的整数运算,提高推理速度。
- 降低内存占用:激活值的量化,可以减少推理期间激活值所占用的内存大小。
- 模型精度下降:因为量化相关的操作给网络中的值带来了误差,因此会导致模型精度的下降。

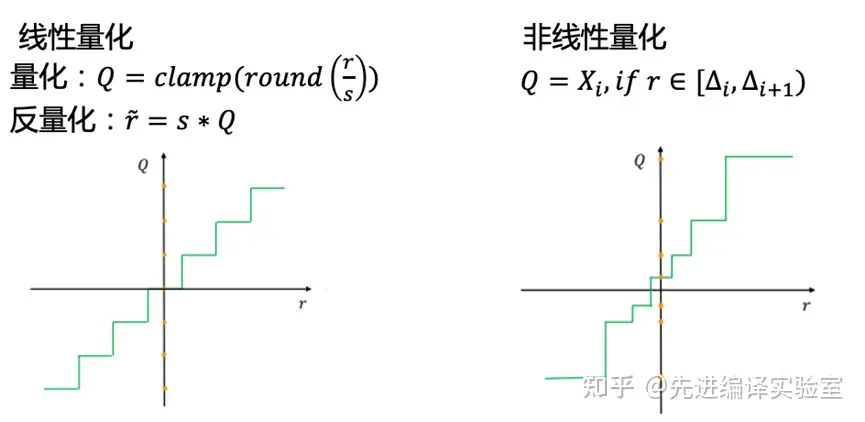
是否线性
由于非线性量化的复杂性,更多使用的是线性量化
是否对称
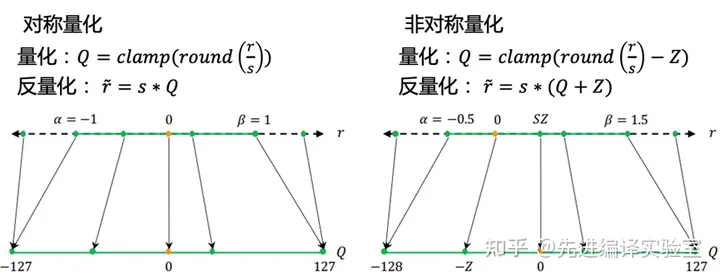
根据浮点值的零点是否映射到量化值的零点,可以将量化分为对称量化和非对称量化。
对称量化:对称量化中浮点值的零点直接映射到量化值的零点,因此不需要其他参数来调整零点的映射的位置,与量化相关的参数只有缩放因子s。对于有符号数的量化(int8),对称量化表示的浮点值范围是关于原点对称的(左图)。对于无符号数量化(uint8),对称量化可以表示的大于等于0的浮点范围。
非对称量化:非对称量化有一个额外的参数Z调整零点的映射,这个参数通常称为零点。非对称量化表示的范围没有严格的限制,可以根据浮点值的范围,选取任意的想要表示的范围。因此非对称量化的效果通常比对称量化好,但是需要额外存储以及推理时计算零点相关的内容。
量化粒度
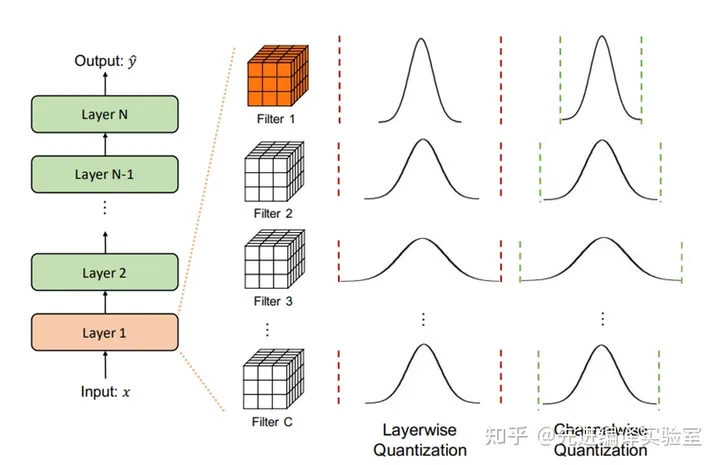
根据量化参数(缩放因子s,零点z)的共享范围,可以将量化分为逐层量化和逐通道量化。
逐层量化:在逐层量化中,每个网络层中的所有filter共享相同的量化参数。所要表示的浮点值范围的选择需要考虑当前层所有的filter来确定。对每层中所有的filter采用相同的范围,对应的缩放因子和零点也是相同的(缩放因子和零点是根据所要表示的浮点值范围和整型值位宽计算得到)。这种方法的实现比较简单,但是它的效果并不是很好,因为不同filter的范围可能会有很大差异。对于范围较小的filter可能会因为同层中存在范围较大的filter而使得其量化效果较差。
逐通道量化:逐通道量化是一种更细粒度的量化方法。在这种方法中,为每层的各个filter单独地计算需要表示的范围以及量化参数。这种方法能够更好的保留每个filter的信息,产生的量化效果也较好。
量化精度
根据网络中量化位宽的不同,可以将量化分为统一精度量化和混合精度量化。
统一精度:在统一精度量化中,所有量化的网络层均采用相同的位宽(相同的整型类型)。这是一种比较简单的精度选择方法,不需要考虑不同层对量化的敏感度。但是采用这种方法,在对网络进行量化或量化到较低精度时,可能会引起网络准确率的显著下降。
混合精度:在混合精度量化中,不同的网络层可以量化到不同的位宽。核心思想是将不适合量化的层保留在较高精度,适合量化的层进行更加激进的量化。使网络整体处于较低位宽,并尽量缓解网络准确率的下降。混合精度量化中需要解决的问题与统一精度类似。但是混合精度量化需要额外关注一点,就是如何决定不同网络层的量化位宽。
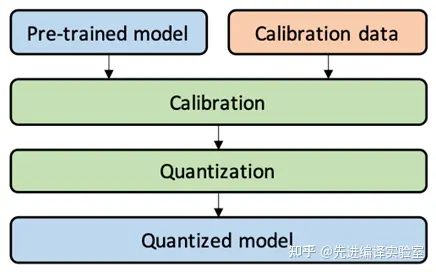
PTQ Post-training quantization
训练后量化直接对已训练完成的模型进行量化,无需复杂的fine-tuning或训练过程,因此训练后量化的开销较小。训练后量化无需或只需要一小部分数据驱动量化,因此能很好地应用于数据敏感的场景。但是训练后量化的模型精度下降可能要高于量化感知训练。训练后量化可以分为权重量化和全量化两种。
权重量化:在权重量化中,仅对模型的权重进行量化操作,以整型形式存储模型权重,可以压缩模型的大小。在推理阶段首先将量化的权重反量化为浮点形式,推理过程仍然为浮点计算,无法加速推理过程,。
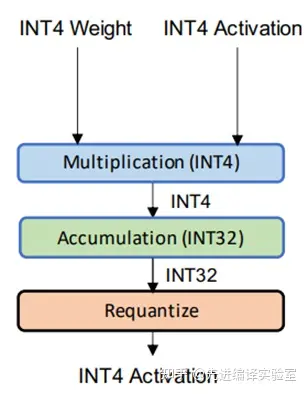
全量化:在全量化中对模型权重和激活值进行量化,不仅可以压缩模型大小,减少推理过程的内存占用,而且因为激活值和权重都为整型数据,因此可以使用高效的整型运算单元加速推理过程。全量化可以分为两种形式:静态量化和动态量化。
- 静态量化:静态量化中离线计算好模型权重和激活的量化参数,推理的时候不再调整直接使用。对激活值量化需要获取激活值的分布信息,因此,静态量化中需要提供一定的数据来推理网络,收集网络的激活值信息,确定相关的量化参数。
- 动态量化:在动态量化中,激活值相关的量化参数是在推理阶段实时计算的。虽然效果更好,但是会给推理带来额外的开销。
QTA Quantization Train aware
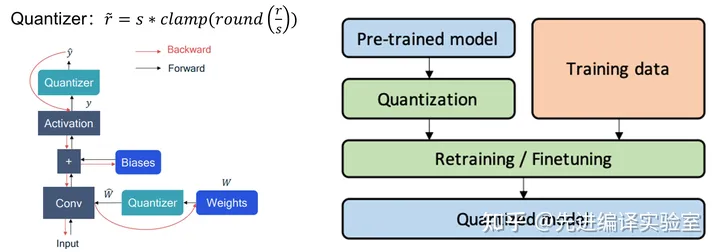
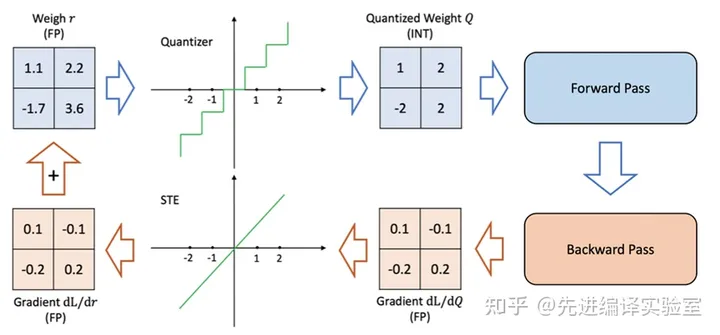
量化感知训练在训练好的模型上插入伪量化算子(对数值量化然后反量化),模拟量化产生的误差。然后在训练数据集更新权重并调整对应的量化参数,或者直接将量化参数作为可学习的参数在反向传播中更新。这种方法得到的量化模型精度较高,但是因为需要训练过程,因此开销较大,而且对于数据的要求相对于训练后量化也更高。
校准方法
校准是调整与确定量化参数的过程。以有符号数对称量化为例,缩放因子
global
max
percentile
mse
kl-divergence